不等式の表す範囲をTikzで描く clipを使う

プリントを作っていて、数学Iの不等式を表す範囲をTikzでうまく描けないか調べていたところ、clip というコマンドがあることを知った。「Tikzで斜線を塗りつぶす方法」というサイトで紹介されていた方法を利用しました。

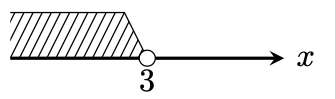
\path[clip] xxxxx と書くと、xxxxxの図形の範囲だけに、図形を書くことができるというものです。上の図でいうと数直線上の台形の図形の範囲を区切って、斜線を沢山書くという方法になります。ただし、その上に白丸を乗せたりする関係で、\begin{scope}と\end{scope}で挟まれたローカルオプションの部分だけで、斜線を描くという限定を指示する必要があります。上の図を描くには次のようにtikzを書いてやることになります。

\begin{tikzpicture}[scale=0.5]
\begin{scope}　　% ここからscope ローカルオプション範囲
\path[clip] (0,0)--(3,0)--(2.5,1)--(0,1)--cycle;　　% 台形の範囲をクリップ
\foreach \t in {-2,-1.8,...,3}{                    % 斜線を-2から3まで0.2刻みで描く
    \path[draw] (\t, 0) -- (\t + 0.5, 1);
  }
\end{scope}　% ここまでscope ローカルオプション範囲
  \draw [line width=1pt,-stealth](0,0)--(6,0)node[right]{$x$};   % 数直線を描く
  \draw (3,0)--(2.5,1)--(0,1);                                   % 台形の外枠を描く
  \draw [fill=white](3,0) circle(5pt)node[below]{3};            % (3,0)の点に白丸を描く
  \end{tikzpicture}

スコープを２つ使えば、不等式の範囲の重なりも表現できます。

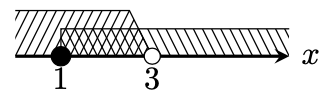
\begin{tikzpicture}[scale=0.5]
\begin{scope}　　% ここからscope1
\path[clip] (0,0)--(3,0)--(2.5,1)--(0,1)--cycle;
\foreach \t in {-2,-1.8,...,3}{
    \path[draw] (¥t, 0) -- (\t + 0.5, 1);
  }
\end{scope}    % ここまでscope1

\begin{scope}　　% ここからscope2
\path[clip] (1,0)--(6,0)--(6,0.6)--(1,0.6)--cycle;
\foreach ¥t in {1,1.2,...,7}{
    \path[draw] (¥t, 0) -- (¥t - 0.5, 1);
  }
¥end{scope}    % ここまでscope2
  
  ¥draw [line width=1pt,-stealth](0,0)--(6,0)node[right]{$x$};
  ¥draw (3,0)--(2.5,1)--(0,1);
  ¥draw (1,0)--(1,0.6)--(6,0.6);
  ¥draw [fill=white](3,0) circle(5pt)node[below]{3};
  ¥draw [fill=black](1,0) circle(6pt)node[below]{¥color{black}1};
  ¥end{tikzpicture}

これを利用すれば、ベン図の交わりも表現できるとのこと。ここを参考にしました。

\begin{tikzpicture}
\draw (0,0) circle[radius=1cm];
\draw[clip] (1,0) circle[radius=1cm];      %  (1,0)中心の円の範囲をクリップ
\fill[lightgray] (0,0) circle[radius=1cm]; %  (0,0)中心の円の中をグレーにする
\end{tikzpicture}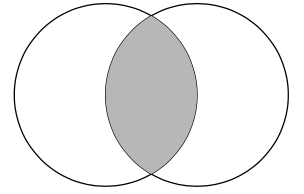

新しいことを知ると、いろいろとできるようになることが、楽しいです。また、情報を共有してくれている方がいらっしゃるということが本当にありがたいです。